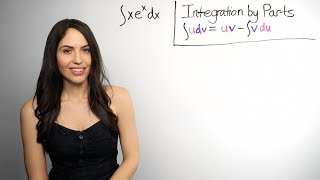Channel: NancyPi

Category: Education

Tags: how tosubstitutionconstantmathematicssimultaneous equationsalgebraexplainedsubstitutetipsexampleinfinitely many solutionshow-toproblemfindfunctionintrosystems of equationscalculatetutorialhow do yougcseintroductionno solutionexpressionmethodtestprecalculuslinear equationequationnancyconsistentsystem of linear equationsinconsistenttutorhelpsystemdistributive propertysolve by substitutionsolvenancypimathsimplifysystem of equations

Description: MIT grad shows how to use the substitution method to solve a system of linear equations (aka. simultaneous equations). To skip ahead: 1) For a BASIC SUBSTITUTION example, skip to time 0:19. 2) For an example where it's TRICKIER to solve and also involves FRACTIONS, skip to 08:17. and P.S.) For WEIRDER-LOOKING DIFFERENT FORMS of systems, for which you can still use substitution, skip to 16:46. Nancy formerly of MathBFF explains the steps. Follow me on Instagram! instagram.com/mathnancy Follow me on Twitter: twitter.com/nancypi For how to solve a system of linear equations with the ELIMINATION METHOD, jump to: youtu.be/XOJgzW4P7T8 What does it mean to solve a system of equations using the SUBSTITUTION METHOD? It means to solve for the x and y values that make both equations true, using the substitution method. Substitution is just one way of solving (elimination is another way). Here are the THREE STEPS you can always follow: STEP 1) First, solve for x or y in either of the two equations in the system (get x or y alone on one side). It doesn't matter which equation you use first, and it doesn't matter whether you get x alone first or y alone first. You can pick whatever looks easiest to solve for in the system. STEP 2) Then, take the expression you found for y (or x) and plug it into the other equation you haven't used yet. For instance, if you got y alone in the first step, take that expression for y and plug it into, or substitute it into, the variable y in the other original equation in the system. Then, simplify the expression by distributing to open up the parentheses (using the distributive property) and combining like terms. Solve for the unknown variable in this equation. STEP 3) Finally, once you solve and get an actual number for a variable, you can take that number and plug it back into either original equation in the system and then simplify and solve for the other variable. This (x,y) pair is your solution. IMPORTANT: If you get something like 0 = 0 or 8 = 8, or something like 1 = 2 or 0 = 21 when you are following these steps and trying to solve, then you've probably found a special case. If you get something TRUE like 0 = 0 (a number equals the same number), then there are an infinite number of solutions to the system, and you can just write "infinitely-many solutions". If instead you get something FALSE like 0 = 21, then there is no solution (inconsistent system), and you can write "no solution". For more of my math videos, check out: nancypi.com